Indice
In matematica, un sistema a due incognite presenta due espressioni matematiche che coinvolgono due variabili, di cui però non potremo conoscere il valore fino al termine della risoluzione del sistema stesso. Nell’articolo di oggi vedremo proprio come fare a risolverlo, cioè a scoprire il valore delle due grandezze che è inizialmente ignoto.
Passo 1
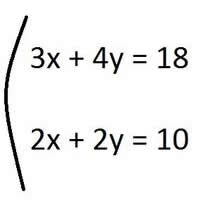 Consideriamo, ad esempio, il sistema di equazioni così costituito: la prima equazione è 3x + 4y = 18, mentre la seconda è rappresentata dall’espressione 2x + 2y = 10. In generale, essendo presenti due equazioni di primo grado (dato che non sono presenti elevamenti a potenza di incognite), dove le grandezze non conosciute sono esattamente due (rappresentate dalle lettere x e y), potete sempre concludere che la soluzione è individuabile.
Consideriamo, ad esempio, il sistema di equazioni così costituito: la prima equazione è 3x + 4y = 18, mentre la seconda è rappresentata dall’espressione 2x + 2y = 10. In generale, essendo presenti due equazioni di primo grado (dato che non sono presenti elevamenti a potenza di incognite), dove le grandezze non conosciute sono esattamente due (rappresentate dalle lettere x e y), potete sempre concludere che la soluzione è individuabile.
passo 2
Per risolvere questo sistema dovremo partire la nostra analisi dalla seconda equazione, ovvero 2x + 2y = 10. Sfruttando la proprietà associativa della somma, questa equazione si potrebbe riscrivere come 2*(x + y) = 10. Quindi, attraverso un semplice passaggio algebrico (divisione per due di entrambi i membri dell’equazione corrente) potremo anche dire che (x + y) = 10 / 2 = 5. E anche che, di conseguenza, x sarà uguale a 5-y.
passo 3
L’informazione ricavata al passo precedente è molto importante! Infatti, ora potremo tornare a concentrare la nostra attenzione sulla prima equazione del sistema, cioè 3x+4y =18, sostituendo al posto della variabile x, proprio 5 – y. Riassumendo, ora sappiamo che 3*(5 – y) + 4y = 18. Quindi, 15 – 3y + 4y = 18. Ora, spostando il primo termine (cioè il numero 15) nel secondo membro dell’equazione, opportunamente cambiato di segno e sommando algebricamente i moltiplicatori di y (-3 +4), ricaviamo finalmente proprio il valore della y, che sarà infatti uguale a 3. Dato che conoscevamo già che x = 5 – y, allora possiamo ottenere anche il valore di x, ovvero 5 – 3 = 2. Dato che adesso abbiamo scoperto il valore delle due incognite, possiamo tranquillamente affermare di essere arrivati alla soluzione del nostro sistema!
Corsi d'Inglese Online
- Corso d'inglese per principianti
- Corso d'inglese per fare carriera prepararsi per un colloquio in inglese - per utenti non madrelingua inglese
- Corso di grammatica ingleseGrammatica base ed intermedia- per utenti non madrelingua inglese
- Corso per scrivere e-mail di lavoro chiare ed efficaci in inglese

Be the first to comment on "Come calcolare un sistema a due incognite"