Indice
In analisi matematica, l’integrale è un operatore che, nel caso di una funzione di una sola variabile, associa alla funzione l’area sottesa dal suo grafico entro un dato intervallo nel dominio. In pratica, si tratta dell’operazione inversa a quella di derivazione: è il processo con cui si calcola l’area sotto una curva delimitata dagli assi x e y del piano. In matematica, esistono regole diverse per gli integrali, a seconda del tipo di polinomio presente.
Integrazione Semplice
Questa regola riguarda i polinomi più elementari. Prendiamo ad esempio il polinomio y = a*x^n.
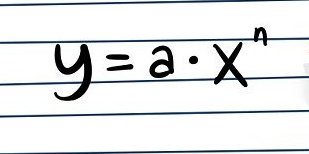
Per risolvere questo integrale, bisogna dividere a (il coefficiente) per n + 1 (l’esponente della potenza + 1) e aggiungere 1. In altre parole, l’integrazione di y = a*x^n è y = (a/n+1)*x^(n+1)…..
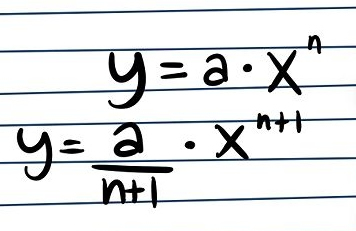
Ora dovremo solo aggiungere la costante di integrazione C con gli integrali indefiniti, così da correggere la sua intrinseca ambiguità per quanto riguarda il valore esatto. Quindi, la soluzione del nostro integrale sarà y = (a/n+1)*x^(n+1) + C…..
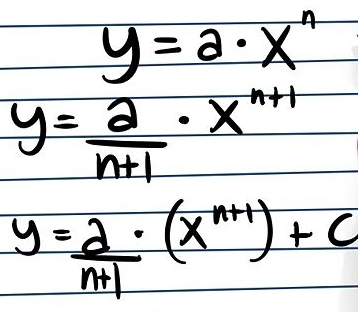
Facciamo ora un esempio più specifico del metodo appena visto: l’integrale di y = 4x^3 + 5x^2 + 3x è (4/4) x^4 + (5/3) * x^3 + (3/2) * x^2 + C = x^4 + (5/3) * x^3 + (3/2) * x^2 + C……
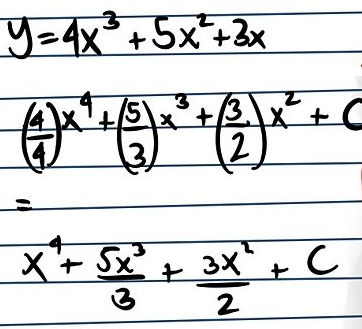
Altri Metodi Di Calcolo
Il metodo di calcolo sopra citato, non è valido quando si hanno degli integrali del tipo x^-1 o 1 / x. Questo perché, quando si integra una variabile con esponente -1, l’integrale è il logaritmo naturale del modulo della variabile. In pratica, l’integrale di (x + 3)^-1 è ln|x+3| + C.
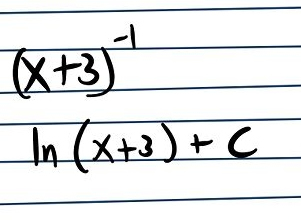
Quindi, l’integrale di e^x…….è sempre se stesso! Mentre, l’integrale di e^(nx) è 1/n * e^(nx) + C, così l’integrale di e^(4x) è 1/4 * e^(4x) + C…..
Invece, l’integrazione di funzioni trigonometriche richiede la conoscenza di alcune regole fondamentali. Tra cui, cos(x) = sen(x) + C
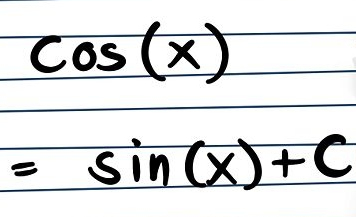
Ricordate anche che l’integrale di sen(x) = – cos(x) + C.
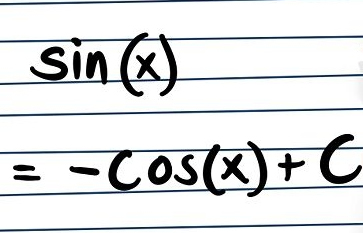
Tenendo a mente queste due regole è possibile ottenere l’integrale della tangente tg(x), sapendo che essa equivale a sen(x)/cos(x). La risposta è – ln|cos x| + C…..
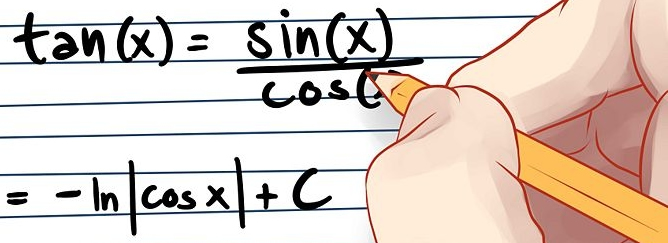
Per quanto riguarda invece i polinomi più complessi, come ad esempio (3x – 5)^4, bisogna integrare per sostituzione. Questa tecnica introduce una variabile, ad esempio u, per sostituire una variabile a più termini, ad esempio 3x – 5: in questo modo, potrete semplificare il processo applicando le stesse regole dell’integrazione di base…..
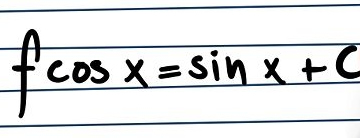
Corsi d'Inglese Online
- Corso d'inglese per principianti
- Corso d'inglese per fare carriera prepararsi per un colloquio in inglese - per utenti non madrelingua inglese
- Corso di grammatica ingleseGrammatica base ed intermedia- per utenti non madrelingua inglese
- Corso per scrivere e-mail di lavoro chiare ed efficaci in inglese

Be the first to comment on "Come Calcolare Gli Integrali Immediati"